Question

For which equation would x = 1 not be a solution?options:x\3 = 3x\1 = 1 x\4= 1\4 x\2 = 2\4

Answer 1

x/3 = 3

Explanation

Substituting x = 1 into the second equation:

`\begin{gathered} (x)/(1)=1 \\ (1)/(1)=1 \\ \text{ Simplifying} \\ 1=1 \end{gathered}`

Given that the same result is obtained at both sides of the equation, then x = 1 is a solution to the equation.

Substituting x = 1 into the third equation:

`\begin{gathered} (x)/(4)=(1)/(4) \\ (1)/(4)=(1)/(4) \end{gathered}`

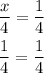
Given that the same result is obtained at both sides of the equation, then x = 1 is a solution to the equation.

Substituting x = 1 into the fourth equation:

`\begin{gathered} (x)/(2)=(2)/(4) \\ (1)/(2)=(2)/(4)\text{ } \\ \text{ Simplifying} \\ (1)/(2)=(1)/(2) \end{gathered}`

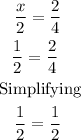
Given that the same result is obtained at both sides of the equation, then x = 1 is a solution to the equation.

Substituting x = 1 into the first equation:

`\begin{gathered} (x)/(3)=3 \\ (1)/(3)\\e3 \end{gathered}`

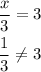
Given that different results are obtained at both sides of the equation, then x = 1 is not a solution to the equation.