Question

Mr. Baldwin brought in 8 solid colored eggs for his Physics classes. 6 of the eggs were yellow If Mr. Baldwin randomly chose 5 eggs for his first class to use in an egg drop experiment, what is the probability that all of them are yellow? Write your answer as a decimal rounded to four decimal places. Can you explain to me how exactly I do this?

Answer 1

The probability that each choice is yellow is 0.1071

Problem Statement

The question says Mr. Baldwin brought 8 solid-colored eggs to his class (6 of which were yellow). We are then asked to find the probability that all the 5 eggs he picked randomly are yellow.

Method

Firstly, we are told that 6 out of the 8 eggs are yellow. This means that the remaining two eggs are NOT yellow. Therefore, we can write a probability of picking from this pool of 8 eggs.

`\begin{gathered} \text{probability of event A= }\frac{\text{possible event A}}{\text{Total number of all possible events}} \\ \text{ number of yellow eggs = 6} \\ \text{ number of NOT yellow eggs = 2} \\ \text{ Total number of eggs = 8} \\ \\ \therefore P(\text{yellow eggs)= }(6)/(8) \\ P(\text{NOT yellow eggs) = }(2)/(8) \end{gathered}`

To solve this question, we need to analyze each scenario as Mr. Baldwin picks each egg.

Implementation

Scenario 1

The first scenario to consider is when Mr. Baldwin picks the first egg. The chance of him picking a yellow egg is 6/8 as shown above.

Thus, for this scenario, the probability of Mr. Baldwin picking a yellow egg is:

`P_1=(6)/(8)`

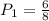
Scenario 2

The eggs are used for an egg drop experiment, meaning that the eggs are not being replaced (since eggs break when dropped). Thus, the total number of eggs has dropped from 8 to 7. Also, because Mr. Baldwin picked a yellow egg in scenario 1, the number of yellow eggs has also reduced from 6 to 5 and as a result, the probability of choosing another yellow egg has changed from its initial value of 6/8.

We can calculate the new probability using the formula above:

`\begin{gathered} P(\text{yellow eggs)= }(5)/(7) \\ P(\text{NOT yellow eggs) = }(2)/(7) \end{gathered}`

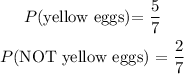
Thus, if Mr. Baldwin chooses another yellow egg for scenario 2, then that probability can be written as:

`P_2=(5)/(7)`

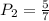
Scenario 3:

We just follow the same pattern as before. The number of eggs has reduced once more from 7 to 6 and the number of yellow eggs has also reduced from 5 to 4.

Thus, the probabilities are:

`\begin{gathered} P(\text{yellow eggs)= }(4)/(6) \\ P(\text{NOT yellow eggs) = }(2)/(6) \\ \\ \therefore P_3=(4)/(6) \end{gathered}`

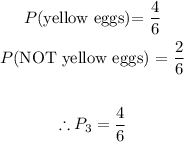
Scenario 4:

The number of eggs has reduced from 6 to 5 and the number of yellow eggs has reduced from 4 to 3.

Thus, the probabilities are:

`\begin{gathered} P(\text{yellow eggs) = }(3)/(5) \\ P(\text{NOT yellow eggs) = }(2)/(5) \\ \\ \therefore P_4=(3)/(5) \end{gathered}`

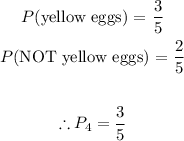
Scenario 5:

Finally, the number of eggs will have reduced from 5 to 4 and the number of yellow eggs has reduced from 3 to 2.

`\begin{gathered} P(\text{yellow eggs) = }(2)/(4) \\ P(\text{NOT yellow eggs) = }(2)/(4) \\ \\ \therefore P_5=(2)/(4) \end{gathered}`

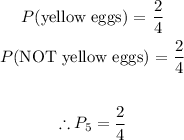
Now that we have all the probabilities of Mr. Baldwin choosing a yellow egg, we can apply the AND probability formula to combine

each of the probabilities.

The AND probability is used when two or more non-mutually exclusive scenarios occur and we are required to find their cumulative probability if they occur together (i.e. at the same time or one after the other like in this case)

The AND probability is given as:

`P(A\text{ AND B) = P(A) }* P(B)`

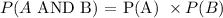
Let us now apply this formula:

`\begin{gathered} P(\text{yellow = 6 AND 5 AND }\ldots2)=(6)/(8)*(5)/(7)*(4)/(6)*(3)/(5)*(2)/(4)=(720)/(6720) \\ \\ \therefore P=0.1071\text{ (to 4 decimal Places)} \end{gathered}`

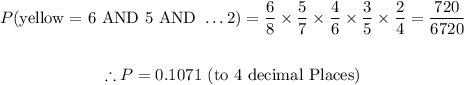
Final Answer

The probability that each choice is yellow is: 0.1071