Annuities
The new home costs $136,000.
2. The down payment is 10%:
DP = 10 * $136,000 / 100 = $13,600
The down payment is $13,600
3. Once he pays the down payment, the amount to borrow is:
$136,000 - $13,600 = $122,400.
He is going to borrow $122,400.
4. Now we need to use the annuities formula for A = $122,400, t = 30 years, r = 3.5%, monthly payments.
The formula is:
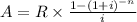
Where:
R = Amount of the monthly payments
i = Monthly rate of interest
n = Number of payments
Solving for R:
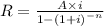
Calculate:

I will keep all the decimals in the calculator. Only a few are shown.
n = 10 years * 12 months per year = 120 payments.
Calculate the amount of the monthly payments:
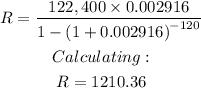
The monthly payments would be $1,210.36
5. The final value of the mortgage is given by:
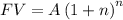
Substituting:
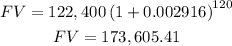
The interest paid is:
I = FV - A
I = $173,605.41 - $122,400
I = $51,205.41
He would pay $51,205.41 in interest over the lifetime of the mortgage