Question

Please helpfind the rate at which the water level is rising in the cistern…

Answer 1

Let r be the radius of the part of the cone filled with water and let h be the height. Then,

`\begin{gathered} (h)/(7)=(r)/(4) \\ h=(7r)/(4) \end{gathered}`

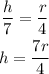
In ten minutes the volume, V, of the part of the cone filled with water is given by

`V=0.065*10=0.65m^3`

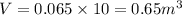
Therefore,

`\begin{gathered} (1)/(3)\pi* r^2*((7r)/(4))=0.65 \\ r_(10m)=0.354688m \\ h_(10m)=0.620704m \end{gathered}`

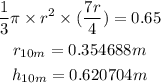
We are given that, the rate at which the cone is being filled is given by

`(dV)/(dt)=0.065m^3\text{ /min}`
`\begin{gathered} V=(1)/(3)\pi r^2h \\ But\text{ }r=(4h)/(7) \\ \text{therefore} \\ V=(16\pi)/(147)h^3 \\ (dV)/(dt)=(16\pi)/(49)\frac{h^2dh}{\text{ dt}} \\ (dh)/(dt)=0.065*(49)/(16\pi(0.620704)^2)=0.164464m\text{ /min} \end{gathered}`

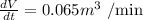
Hence, the rate at which the water level is rising is 0.164 meters per minute