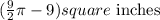Solution:
Given that the square has sides 6'' and is inscribed in a circle, the figure is as shown below:
Step 1: Evaluate the length of the diagonal BD.
Thus, from the Pythagorean theorem,
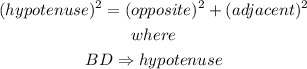
Thus,
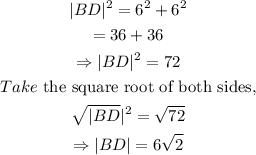
Step 2: Evaluate the radius of the circle.
The radius of the circle is exactly half the length of the diagonal.
Thus,

Step 3: Evaluate the area of the circle.
The area of the circle is expressed as

Step 4: Evaluate the area of the square.
The area of a square is evaluated as

Step 5: Subtract the area of the square from the area of the circle.
Thus,
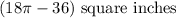
Step 6: Divide the obtained area by the number of segments.
The obtained area is the total area of the segments in the above figure.
Thus, to obtain the area of one segment, we divide by the total number of segments.
Thus,
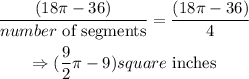
Hence, the area of one segment formed by the square is