Question

A man ordered 3 times as many boxes of ballpoint pens as boxes of felt tip pens. Ballpoint pens cost $4.35 per box and felt tip pens cost $3.43. If the man's order of pens totaled $65.92 how many boxes of each type of pen did he buy?

Answer 1

The first step to solve the problem is assigning variables to each type of pen. We will call ballpoint "x" and felt tips "y". We know that each box of ballpoint cost $4.35, if we multiply the number of ballpoint boxes, x, by the price of each box we should have the value spent on that kind of pen, the same can be applied to felt tip pens, when we add both of these, the result should be equal to $65.92.

`4.35\cdot x+3.43\cdot y=65.92`

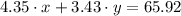
We know that he ordered 3 times as many boxes of ballpoints as felt tips. Therefore we have:

`x=3\cdot y`

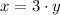
If we replace "x" on the first equation with the second equation, we can solve for y.

`\begin{gathered} 4.35\cdot(3\cdot y)+3.43\cdot y=65.92 \\ 13.05\cdot y+3.43\cdot y=65.92 \\ 16.48\cdot y=65.92 \\ y=(65.92)/(16.48)=4 \end{gathered}`

Using the second equation, we can find the value of x.

`x=3\cdot4=12`

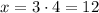
He bought a total of 12 ballpoint boxes and 4 felt tip boxes.