SOLUTION
Step1
Define the parameters for the given information
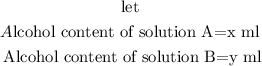
Step2
Write out the equation for the information given
He uses twice as much solution A as solution B is written as
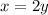
Then
Solution A is 16% alcohol and solution B is 19% we have
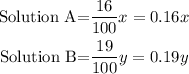
For the mixture to have 480ml of alcohol, we have
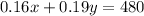
Step3
Solve the equation simultaneously

substitute equation (1) into equation (2)
we have
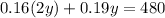
expand the parenthesis
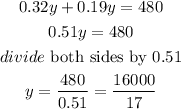
Then the value of becomes
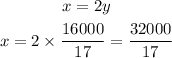
Therefore
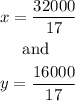
Hence
Jose will needs 1882.35ml of solution A and 941.18ml of solution B