Let x be the first number and y be the second number.
Given, the first number minus the second number is 154. Therefore,
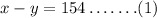
Given, 3 times the first number plus two times the second number is 358. Therefore,
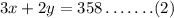
Multiply equation (1) by 2.
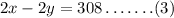
Now, add equations (2) and (3) to find x.
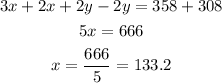
Put x=133.2 in equation (1) to find y.
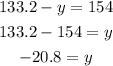
Therefore, the first number x is 133.2 and the second number y is -20.8.
To check the answer, put y=-20.8 and x=133.2 in equation (1) and check if the left hand side of equation equals right hand side of equation.
LHS of equ. (1) is,
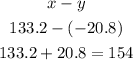
We know, RHS of equ. (1) is 154.
So, LHS=RHS, and hence, the x and y values satisfies the equation.