Answer:
t = 0.118 seconds
Explanation:
The vertical distance in a straight-up motion of the ball is described by
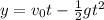
where
v0 = vertical velocity of the ball
g = acceleration due to gravity
t = time after the launch
Now in our case, v_0 = 17.6 m/s and g= 9.8 m/s^2; therefore,
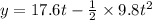
When the ball crosses the height of 2m, we have y = 2; therefore, the above equation gives
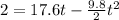
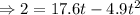
subtracting 2 from both sides gives

The above can be rewritten in a more familiar form by a bit of rearranging of the terms.
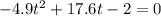
This is a quadratic equation, and therefore, the values of t can be found using the quadratic formula.
Using the quadratic formula, we get two possible values of t:
![t=\frac{-17.6\pm\sqrt[]{17.6^2-4(-4.9)(-2)}}{2*(-4.9)}](https://img.qammunity.org/2023/formulas/physics/college/t7xgrvjv9yy1toj4wy55x0ob8f00fzcyxm.png)
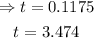
Which value of t is correct?
The two values of t tell us that the ball crosses the y = 2 checkpoint twice. First when going up and second when coming down. Since we want the time when the ball is going up, we choose t= 0.1175 (because the ball goes up first and then it comes down).
Hence, after 0.118s (rounded to the nearest thousandth), the ball crosses the height of 2m going up.