Question

The future value when interest is compounded semiannually is approximately $?

Answer 1

Part a)Explanation

Finding the future value

The future value when the interest is compounded semiannually can be determined using the following formula.

`\begin{gathered} A=P(1+(r)/(n))^(tn) \\ \text{ Where} \\ P\text{ is the amount invested} \\ r\text{ is the rate of interest } \\ n\text{ is the number of times per year the interest is compounded} \\ t\text{ is the number of years for which the principal is invested} \end{gathered}`

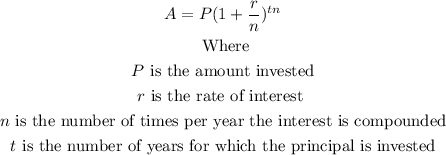
Then, we have:

`\begin{gathered} A=? \\ P=8704.56 \\ r=6\%=(6)/(100)=0.06 \\ n=2\text{ Because the interest is compounded semiannually} \\ t=9 \end{gathered}`

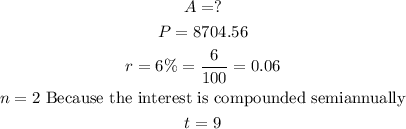
Now, we replace the values in the formula.

`\begin{gathered} A=P(1+(r)/(n))^(tn) \\ A=8704.56(1+(0.06)/(2))^(2*9) \\ A=8704.56(1+0.03)^(18) \\ A=14818.93 \end{gathered}`

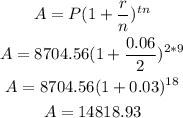
Finding the interest earned

`\begin{gathered} \text{ Interest earned }=\text{ Future Value}-\text{ Present Value} \\ \text{ Interest earned }=14818.93-8704.56 \\ \text{ Interest earned }=6114.37 \end{gathered}`Answer

The future value when interest is compounded semiannually is approximately $14818.93, and the interest earned is $6114.37.

Part b)Explanation

Finding the future value

The future value when the interest is compounded continuously can be determined using the following formula.

`\begin{gathered} A=Pe^(rt) \\ \text{ Where} \\ P\text{ is the amount invested} \\ r\text{ is the interest rate in decimal form} \\ \text{t is the number of years for which the principal is invested} \end{gathered}`

Then, we have:

`\begin{gathered} P=8704.56 \\ r=0.06 \\ t=9 \end{gathered}`

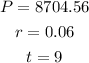
Now, we replace the values in the formula.

`\begin{gathered} A=Pe^(rt) \\ A=8704.56*e^(0.06*9) \\ A=14937.08 \end{gathered}`

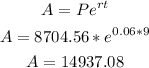
Finding the interest earned

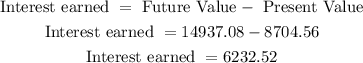
`\begin{gathered} \text{ Interest earned }=\text{ Future Value}-\text{ Present Value} \\ \text{ Interest earned }=14937.08-8704.56 \\ \text{ Interest earned }=6232.52 \end{gathered}`Answer

The future value when interest is compounded semiannually is approximately $14937.08, and the interest earned is $6232.52.