Question

+The population P (in thousands) of a country can be modeled by the function below, where t is time in years, with t = 0 corresponding to 1980.P = -14.04 + 781.17 + 167,983(a) Evaluate P for t = 0, 10, 15, 20, and 25.P(O) -peopleP(10) -peopleP(15) -peopleP(20) =peopleP(25) -peopleExplain these valuesThe Select is Select -- 0(b) Determine the population growth rate, dP/dt.dP/dt =(c) Evaluate d/dt for the same values as in part (a).P(0)people per yearP (10) -people per yearP'(15) -people per yearP' (20) =people per yearP'(25)people per yearExplain your results,The Select Is-Select

Answer 1

Given:

The population P (in thousands) of a country can be modeled by the function below, where t is time in years, with t = 0 corresponding to 1980.

`P=-14.04t^2+781.17t+167,983`

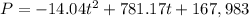
Part A:

we will find P for t = 0, 10, 15, 20, and 25.

So, substitute each value of (t) and calculate the corresponding value of P as follows:

`\begin{gathered} t=0\rightarrow P=-14.04(0)^2+781.17(0)+167,983=167983 \\ t=10\rightarrow P=-14.04(10)^2+781.17(10)+167,983=174390 \\ t=15\rightarrow P=-14.04(15)^2+781.17(15)+167,983=176540.5 \\ t=20\rightarrow P=-14.04(20)^2+781.17(20)+167,983=177989 \\ t=25\rightarrow P=-14.04(25)^2+781.17(25)+167,983=178735.5 \end{gathered}`

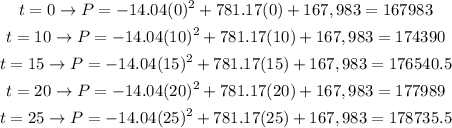
So, the answer will be:

P(0) = 167983

P(10) = 174390

P(15) = 176540.5

P(20) = 177989

P(25) = 178735.5

===========================================================

Part B:

We will find the population growth rate dP/dt:

So, we will find the first derivative from the given equation as follows:

`\begin{gathered} (dP)/(dt)=-14.04(2t)+781.1(1)+0 \\ \end{gathered}`

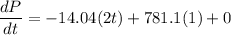
So, the answer will be:

`(dP)/(dt)=-28.08t+781.1`

==========================================================

Part C:

We will evaluate dP/dt for the same values as in part A

So, we will find dP/dt for t = 0, 10, 15, 20, and 25.

So, substitute each value of (t) and calculate the corresponding value of dP/dt as follows:

`\begin{gathered} t=0\rightarrow(dP)/(dt)=-28.08(0)+781.1=781.1 \\ \\ t=10\rightarrow(dP)/(dt)=-28.08(10)+781.1=500.3 \\ \\ t=15\rightarrow(dP)/(dt)=-28.08(15)+781.1=359.9 \\ \\ t=20\rightarrow(dP)/(dt)=-28.08(20)+781.1=219.5 \\ \\ t=25\rightarrow(dP)/(dt)=-28.08(25)+781.1=79.1 \end{gathered}`

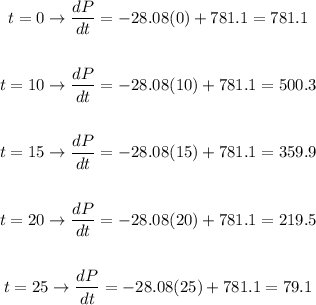
So, the answer will be:

P'(0) = 781.1

P'(10) = 500.3

P'(15) = 359.9

P'(20) = 219.5

P'(25) = 79.1

The rate of growth is decreasing.