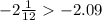Question

Replace the ● with <, > or = to make a true sentence?

Answer 1

`-2(1)/(12)>-2.09`

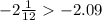
SOLUTION

Problem Statement

The question asks us to insert the correct operator symbol depending on which number is greater, smaller or whether the two numbers are equal

The numbers given are:

`\begin{gathered} -2(1)/(12)\text{ and} \\ \\ \text{ }-2.09 \end{gathered}`

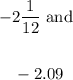
Solution

To solve this problem, we need to ensure the two numbers are in the same form. Either they are both decimals or they are both fractions.

For this solution, we should make the fraction into a decimal and then compare the two numbers.

We should note that for negative numbers if a negative number is larger in magnitude than another negative number, then the negative number with the larger magnitude is actually the smaller number.

To illustrate this, take the following example:

`\begin{gathered} \text{ Comparing -5 with -3;} \\ -5\text{ has a magnitude of 5 and -3 has a magnitude of 3} \\ \text{This means that -5 is SMALLER THAN -3} \end{gathered}`

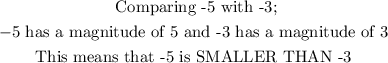
Now that we understand the logic to use to solve the question, we can proceed to solve the question.

Let us now convert the fraction into a decimal:

After this, we can now compare the two numbers:

`\begin{gathered} \text{Comparing }-2.08\bar{3}\text{ and }-2.09 \\ The\text{ magnitude of }-2.08\bar{3}\text{ is }2.08\bar{3} \\ \text{The magnitude of }-2.09\text{ is }2.09 \\ 2.09\text{ is greater than 2.08}\bar{3}\text{ in magnitude} \\ \\ \therefore-2.08\bar{3}\text{ is greater than -2.09} \end{gathered}`

Therefore, the solution is:

`-2(1)/(12)>-2.09`