We know that we can relate the Forces and the areas on which they are applied in a hydraulic jack by the formula:
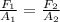
In this case let F1 by the input force. We know that the area of the cylinders is given by:

We know that the radius of the input cylinder is 4.5 cm and the radius of the output cylinder is 9.5 cm. We also know that the force we required is 3500 N; then we have:
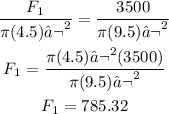
Therefore, the input force we need to exert is 785.32 N