In this case, we can identify two similar triangles like this:
Since VX is a bisector of ZC it cuts ZC into two equal-length segments, then ZY and YC have the same length and we can formulate the following expression:
ZY = YC
ZY = 18
Since we are dealing with similar triangles, we can formulate the following expressions for VYZ and ZYX:
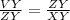
By replacing 18 for ZY and 27 for XY, we get:
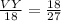
By multiplying both sides by 18, we can solve for 18, to get:
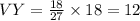
By adding the length of VY to the length of XY, we get:
VY + XY = 12 + 27 = 39
Adding VY to XY we should get VX, which is the diameter of the circle. Then VX = 39