Question

Solve each system by elimination.2x + 5y = -243x - 5y = 141. Which variable has an opposite pair? Type x or y2. Solve for x .3. Substitute the value x of into one of the original equations to solve for y .4. Write the solution as an ordered pair (x,y)( , )

Answer 1

The Solution:

Given the pair of equations below:

`\begin{gathered} 2x+5y=-24 \\ 3x-5y=14 \end{gathered}`

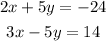
We are asked to solve by the Elimination Method.

1. The variable that has an opposite pair is [variable y]

2. To solve for x, we shall add the corresponding terms in both equations together.

`\begin{gathered} 2x+5y=-24 \\ +(3x-5y=14) \\ ------------ \\ 5x+0=-10 \\ 5x=-10 \end{gathered}`

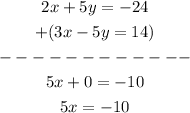
Dividing both sides by 5, we get

`\begin{gathered} (5x)/(5)=(-10)/(5) \\ \\ x=-2 \end{gathered}`

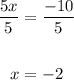
3. Substituting -2 for x in the first equation, to get the value of y.

`\begin{gathered} 2x+5y=-24 \\ 2(-2)+5y=-24 \\ -4+5y=-24 \end{gathered}`

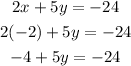
Bringing the like terms to one side, we get

`\begin{gathered} 5y=-24+4 \\ 5y=-20 \end{gathered}`

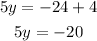
Dividing both sides by 5, we get

`\begin{gathered} (5y)/(5)=(-20)/(5) \\ \\ y=-4 \end{gathered}`

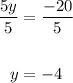
4. Writing the solution as an ordered pair, we have

`(x,y)=(-2,-4)`

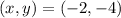
Therefore, the correct answer is (-2 , -4)