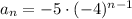Question

-5, 20, -80, 320, ... is a geometric sequence a. Find the common ratio, b. Write its recursive rule c. Write its explicit rule.What is the common ratio and explicit rule?

Answer 1

a.

In order to find the common ratio, we just need to divide a term by the term that comes before it.

So using the terms 20 and -5, we have:

`\text{ratio}=(20)/(-5)=-4`

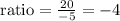
b.

The recursive rule can be found with the formula:

`a_n=a_(n-1)\cdot q`

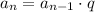
Where an is the nth term and q is the ratio. So we have:

`a_n=a_(n-1)\cdot(-4)`

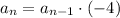
c.

The explicit rule can be written as:

`a_n=a_1\cdot q^(n-1)`

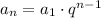
Where an is the nth term, a1 is the first term and q is the ratio. So:

`a_n=-5\cdot(-4)^(n-1)`