Question

Consider the following function. Complete parts (a) through (e) below.f(x)=x²-2x-15b. Find the vertex.The vertex is(Type an ordered pair.)c. Find the x-intercepts. The x-intercept(s) is/are.(Type an integer or a fraction. Use a comma to separate answers as needed.)d. Find the y-intercept. The y-intercept is(Type an integer or a fraction.)e. Use the results from parts (a)-(d) to graph the quadratic function.Graph the parabola using the vertex and an intercent on the tool to the right....

Answer 1

Given: A quadratic equation

`f(x)=x^2-2x-15`

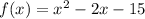
Required: To find the vertex, x-intercepts, y-intercept, and graph the given quadratic function.

Explanation: Comparing the given equation with general quadratic function

`f(x)=ax^2+bx+c\text{ }`

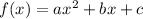
we get, a=1, b=-2, and c=-15. Now the x coordinate of the vertex of the quadratic function is

`x=-(b)/(2a)`

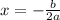
Hence,

`x=1`

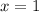
At x=1, f(x) is

`\begin{gathered} f(1)=(1)^2-2(1)-15 \\ =-16 \end{gathered}`

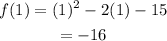
Hence the vertex of the given function is (1,-16). Now for getting the x-intercept we put f(x)=0, i.e.,

`\begin{gathered} x^2-2x-15=0 \\ (x-5)(x+3)=0 \\ x=5\text{ and} \\ x=-3 \end{gathered}`

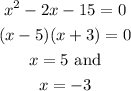
Hence the x-intercepts are (5,0) and (-3,0). Similarly, for y-intercept, we put x=0 and find f(x) as follows

`\begin{gathered} f(0)=0^2-2(0)-15 \\ =-15 \end{gathered}`

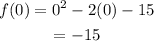
Hence y-intercept is (0,-15). Now using the vertex and intercepts to graph the given quadratic function is shown below.

Final Answer: b) Vertex=(1,-16)

c) x intercepts are (5,0) and (-3,0)

d) y intercepts is (0,-15)

e) The graph of f(x) is shown below.