Given:
![\begin{gathered} Total\text{ N}umber\text{ of sprockets = 37} \\ Number\text{ of defective sprockets = 4} \\ Number\text{ of non-defective sprockets = 33} \end{gathered}]()
Required:
The probability that all in the sample are defective.
The probability that none in the sample is defective.
Step-by-step explanation:
(a) 5 sprockets are selected probability that all are defective favorable cases are 1 which means all 4 are defective.
The number of ways of selecting 4 from 4 defective sprockets is,
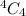
The required probability is calculated as,

Thus the probability that all selected is 1/66045.
(b) The 4 sprockets selected are non-defective.
The number of ways of selecting 4 sprockets is,
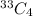
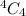
The required probability is calculated as,
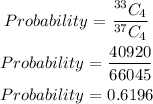
Answer:
Thus the probability that all selected is 1/66045.
Thus the probability of selecting 4 non-defective sprockets is 0.6196.