Question

In a clinical trial of a cholesterol drug,390 subjects were given a placebo, and 23% of them developed headaches. For such randomly selected groups of 390 subjectsgiven a placebo, identify the values of n, p, and q that would be used for finding the mean and standard deviation for the number of subjects who develop headaches

Answer 1

Generally, 'n' represent the sample size, 'p' is the probability of success in a single trial, and 'q' is the corresponding probability of failure in a single trial.

The given problem suggests that the randomly selected group consists of 390 subjects. It follows that the sample size considered contains 390 subjects,

`n=390`

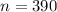
The objective is to study the number of subjects who develop headaches.

So we declare here that the success for a trial is defined as a subject from the group being found to have developed headaches.

Given that 23% of the subjects given a placebo, develop headaches. So the probability that a randomly selected subject will develop headache, that is, the probability of success is given by,

`\begin{gathered} p=23\text{ percent} \\ p=(23)/(100) \\ p=0.23 \end{gathered}`

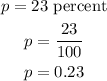
Thus, the value of 'p' is obtained as,

`p=0.23`

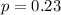
It is known that success and failure are complementary events, so the sum of their probabilities must be unity,

`p+q=1`

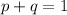
Substitute the value and solve for 'q' as follows,

`\begin{gathered} 0.23+q=1 \\ q=1-0.23 \\ q=0.77 \end{gathered}`

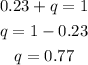
Thus, the value of 'q' is 0.77.