Question

Given a rectangle with length of (2x+9)cm and width of (3x+1)cm.Two squares, each with sides x cm is removed from the rectangle.The remaining shape has an area of 83cm².Find the value of length and width of the rectangle.

​

Answer 1

Answer: The length is 13cm and the width is 7cm

Explanation:

For a rectangle of length L and width W, the area is:

A = W*L

In this case we have:

L = (2*x + 9) cm

W=(3*x + 1) cm

Then the area of the rectangle is:

A = (2*x + 9)*(3*x + 1) cm^2

A = (6*x^2 + 2*x + 27*x + 9) cm^2

A = (6*x^2 + 29*x + 9) cm^2

now we remove two squares with sides of x cm

The area of each one of these squares is (x cm)*(x cm) = x^2 cm^2

Then the area of the figure will be:

area = (6*x^2 + 29*x + 9) cm^2 - (2*x^2 ) cm^2

area = (4*x^2 + 29*x + 9) cm^2

Now we know that the area of this shape is 83 cm^2, then we need to solve:

83 cm^2 = (4*x^2 + 29*x + 9) cm^2

0 = (4*x^2 + 29*x + 9) cm^2 - 83 cm^2

0 = (4*x^2 + 29*x - 74) cm^2

Then we need to solve:

0 = 4*x^2 + 29*x - 74

Here we can use Bhaskara's equation, the solutions of this equation are given by:

`x = (-29 \pm √(29^2 - 4*4*(-74)) )/(2*4) = (-29 \pm 45)/(8)`

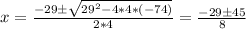
Then the two solutions are:

x = (-29 - 45)/8 = -9.25 (for how the length and width are defined, we can not have x as a negative number, then this solution can be discarded).

The other solution is:

x = (-29 + 45)/8 = 2

x = 2

Then the length and width of the rectangle are:

Length = (2*2 + 9)cm = 13 cm

Width = (3*2 + 1)cm = 7cm