Question

Rewrite the matrix equation as a system of equations in standard form. Is (6, 10) a solution to the system?

Answer 1

Given

`\begin{bmatrix}{3} & {-1} \\ {1} & {2}\end{bmatrix}\begin{bmatrix}{x} & {} \\ {y} & {}\end{bmatrix}=\begin{bmatrix}{8} & {} \\ {5} & {}\end{bmatrix}`

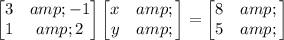
Find

Rewrite as a system of equations in standard form.

Step-by-step explanation

`\begin{gathered} \begin{bmatrix}{3} & {-1} \\ {1} & {2}\end{bmatrix}\begin{bmatrix}{x} & {} \\ {y} & {}\end{bmatrix}=\begin{bmatrix}{8} & {} \\ {5} & {}\end{bmatrix} \\ \\ \begin{bmatrix}{3x-y} & {} \\ {x+2y} & {}\end{bmatrix}=\begin{bmatrix}{8} & {} \\ {5} & {}\end{bmatrix} \end{gathered}`

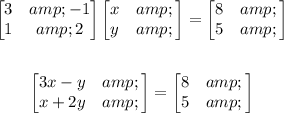
so, ,

`\begin{gathered} 3x-y=8 \\ x+2y=5 \end{gathered}`

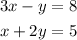
now check (6,10) is solution of both equations .

`\begin{gathered} 3(6)-10=8 \\ 18-10=8 \\ 8=8 \end{gathered}`

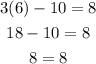
hence , it is the solution of this equation.

now ,

`\begin{gathered} 6+2(10)=5 \\ 6+20=5 \\ 26\\e5 \end{gathered}`

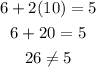
so , it is not solution of this equation.

Final Answer

The correct option is B