Question

An initial investment of $6,200 is worth $18,600 after eight years of continuous compounding. Find theinterest rate. Write it as a percent rounded out 2 decimal places.

Answer 1

Given:

An initial investment of $6,200 is worth $18,600 after eight years of continuous compounding.

Required:

Find the interest rate.

Step-by-step explanation:

We know the continuous compound interest

`A=Pe^(rt)`

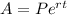
Where, A = Amount (Future value )

P = Principal(Initial rate)

r = Interest rate

t = time

Now,

`\begin{gathered} A=Pe^(rt) \\ 18600=6200e^(r*8) \\ (18600)/(6200)=e^(8r) \\ log(3)=8r \\ r=0.05964 \\ r=0.05964 \\ r=5.96\% \end{gathered}`

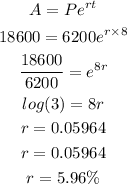
Answer:

The interest rate is 5.96%