Starting from the equation:
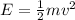
Multiply both members by 2 to cancel out the factor of 1/2 on the right member of the equation:
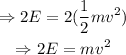
Divide both members by m to cancel out the factor of m on the right member of the equation:
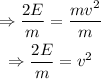
Take the square root of both member of the equation to get rid of the exponent of v:
![\begin{gathered} \Rightarrow\sqrt[]{(2E)/(m)}=\sqrt[]{v^2} \\ \Rightarrow\sqrt[]{(2E)/(m)}=v \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ii6hrbfy19mhqjk6gr5emkk65copt3ts5m.png)
Therefore, the equation rearranged so that it is solved for v is:
![v=\sqrt[]{(2E)/(m)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/bq55vs7wgslsls3dblz9ktkxpasvex5wca.png)