Recall that to graph a line we need two points on the line.
Substituting x=0 in the first equation we get:
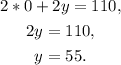
Therefore the graph of the first equation passes through (0,55).
Substituting y=0 in the first equation we get:
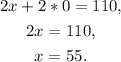
Therefore the graph of the first equation passes through (55,0).
Then, the graph of the first equation is:
Now, substituting x=0 in the second equation we get:
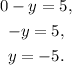
Therefore the second equation passes through (0,-5).
Substituting y=0 in the second equation we get:

Therefore the second equation passes through (5,0).
Then, the graph of the second equation is:
Now, notice that the intersection of both graphs is:
Answer: x=30 and y=25.