Question

If JB and CI are medians and JW=6x+2 and JB=10x+1, calculate the lenght of the segment JW

Answer 1

JB is a median

CI is a median

JW=6x+2

JB=10x+1

If W is the centeroidof the triangle, determined by medians JB, CI and KA, it means that it cuts both line segments following the ratio 2:1 → meaning that the segment JW is 2/3 of the segment JB while the segment WB is 1/3 of JB.

This means that the ratio between segments JW and JB is as follows:

`(2)/(3)=(JW)/(JB)`

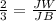
Replece it with the given expressions:

`(2)/(3)=(6x+2)/(10x+1)`

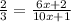
Use cross multiplication between both fractions:

`\begin{gathered} 2\cdot(10x+1)=3(6x+2) \\ 20x+2=18x+6 \end{gathered}`

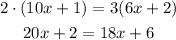
And finally solve for x

`\begin{gathered} 20x-18x=6-2 \\ 2x=4 \\ x=2 \end{gathered}`

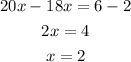
The unknown value is x=2

Now you can calculate the length of segment JW as:

`\begin{gathered} JW=6x+2 \\ JW=6\cdot2+2 \\ JW=14 \end{gathered}`

The length of segment JW is 14 units.