Question

Find the vertex, focus, and directrix of the parabola.(y + 3)^2 = 16(x - 3)

Answer 1

We will have the following:

We are given the parabola:

`(y+3)^2=16(x-3)`

And we can see that it follows:

`(y-k)^2=4p(x-h)`

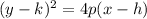
Now, we will have that the vertex is given by:

`(h,k)`

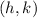
From the equation we then have that the vertex is:

`(3,-3)`

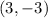
Now, we can see that p = 4 since 16 / 4 = 4. Now, we remember that the focus is located p units to the right since it is positive, thus the focus is given by:

`(h+p,k)`

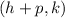
So, the focus is at:

`(3+4,-3)\to(7,-3)`

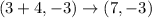
Finally we will have that the directrix of the parabola will be given by:

*First, we find the distance between the focus and the vertex, that is:

`d=\sqrt[]{(7-3)^2+(-3-(-3))^2}\Rightarrow d=4`

Now, since the x coordinate of the vertex is 3, then the directrix will pass at 4 units to its left, that is the directrix is given by:

`x=-1`

That can be seing in the graph:

*** Summary***

Vertex: (3, -3)

Focus: (7, -3)

Directrix: x = -1