Question

When x4 + k is divided by x + 2, the remainder is 3. The value of k is

Answer 1

We are asked to divide the following expressions:

`\begin{gathered} x^4+k \\ x+2 \end{gathered}`

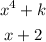
To do that we will use syntetic division. First, we will use the coefficients of each of the powers of "x" in the first expression. If a power of "x" does not appear it means that the coefficient is zero. All those will be divided by the zero of the second expression. Like this:

Now we lower the first coefficient and multiply it by 2 and add that to the second coefficient, like this:

now we repeat this step for the resulting number. Like this:

Now we repeat the step for the result:

Now we repeat the step for the result:

The last number we got "16 + k" is the remainder. The problem says that the remainder must be equal to 3, therefore, we set the remainder to 3:

`16+k=3`

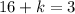
We solve for "k" by subtracting 16 from both side:

`\begin{gathered} k=3-16 \\ k=-13 \end{gathered}`

Therefore, the value of "k" must be -13.