Question

a) What is the maximum height of the ball?(b) How many seconds does it take for the ball to hit the ground?

Answer 1

f(t) = -4.9t² + 24t + 8

a) The maximum height of the ball is given by the value of the function of the vertex of its parabola

For any quadractic function g(x) = ax² + bx + c, its vertex is given by:

`(x_v,y_v)=(-(b)/(2a),-(b^2-4ac)/(4a))_{}`

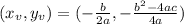
Then, the maximum heigt of the ball is given by:

`\begin{gathered} h_(\max )=-\frac{24^2-4\cdot(-4.9)\cdot8_{}}{4\cdot(-4.9)} \\ h_(max)\approx37.4\text{ m} \end{gathered}`

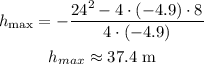
b) When f(t) = 0, we have:

`\begin{gathered} -4.9t^2+24t+8=0 \\ t_{}=\frac{-24\pm\sqrt[]{24^2-4\cdot(-4.9)\cdot8}}{2\cdot(-4.9)} \end{gathered}`

The only positive value is 5.2 (rounded)

Therefore, the ball hit the ground after 5.2 seconds