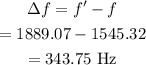Question

Two people hear a 1700 Hz siren of an ambulance. One person is in front of the ambulance, the other is behind the ambulance. If the ambulance is travelling at 120 km/h, what is the difference in frequencies heard by the two people? Assume the speed of sound is 333 m/s.

Answer 1

The original frequency is

`f_o=1700\text{ Hz}`

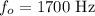
The speed of the ambulance is

`\begin{gathered} v^(\prime)=120\text{ km/h} \\ =120*(5)/(18) \\ =33.33\text{ m/s} \end{gathered}`

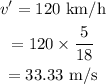
The speed of sound is v = 333 m/s

Let the observer standing behind the ambulance heard the frequency f.

The frequency heard by this observer will be

`\begin{gathered} f=((v)/(v+v^(\prime)))f_o \\ =((333)/(333+33.33))*1700 \\ f=1545.32\text{ Hz} \end{gathered}`

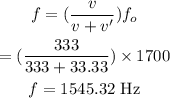
Let the observer standing in front of the ambulance heard the frequency f'.

The frequency heard by this observer will be

`\begin{gathered} f^(\prime)=((v)/(v-v^(\prime)))f_o \\ =((333)/(333-33.33))*1700 \\ f^(\prime)=1889.07\text{ Hz} \end{gathered}`

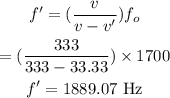
Thus the difference between the frequencies observed by the observers are

`\begin{gathered} \Delta f=f^(\prime)-f \\ =1889.07-1545.32 \\ =343.75\text{ Hz} \end{gathered}`