Question

For each case, apply the big-little principle and/or rules for polynomials to describe the long-term behavior of the function. 1. F(t) = 40t - t^3 Long term behavior of F(t):a. As t increases without bound, F(t) will increase without bound. b. As t increases, F(t) will decrease without bound. c. As t increases without bound, F(t) will approach 0. 2. B(t) = -57/t^2 Long term behavior of B(t): a. As t increases without bound, B(t) will increase without bound. b. As t increases, B(t) will decrease without bound. c. As t increases without bound, B(t) will approach 0.

Answer 1

• 1. b. As t increases, F(t) will decrease without bound.

,

• 2. c. As t increases without bound, B(t) will approach 0.

Explanation:

Part 1

Given the function:

`F\mleft(t\mright)=40t-t^3`

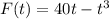
We can rewrite the graph in the standard form below:

`F(t)=-t^3+40t`

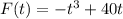
• The ,highest degree is odd, and the leading coefficient is negative, this means that the ,graph rises to the left and falls to the right.

Therefore, As t increases, F(t) will decrease without bound.

Option B is correct.

Part 2

Given the function:

`B(t)=-(57)/(t^2)`

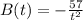
By the big-little principle, if c is a number that is far from 0 on the number line, then 1/c is a number that is close to 0 on the number line.

Thus, as t increases without bound, B(t) will approach 0.

Option C is correct.