Step-by-step explanation
The formula to find the arc length of a circle if the angle is measured in degrees is:
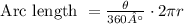
In this case, have:
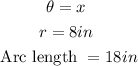
Now, we substitute the know values in the arc length formula and solve for x:
![\begin{gathered} \text{ Arc length }=(\theta)/(360°)\cdot2\pi r \\ 18in=(x)/(360°)\cdot2\pi(8in) \\ 18in=(x)/(360\degree)\cdot16\pi in \\ \text{ Multiply by 360\degree from both sides} \\ 360\degree\cdot18\imaginaryI n=360\degree\cdot\frac{x}{360\operatorname{\degree}}\cdot16\pi\imaginaryI n \\ 360\degree\cdot18\mathrm{i}n=16\pi xin \\ \text{ Divide by }16\pi in\text{ from both sides} \\ \frac{\begin{equation*}360\degree\cdot18\mathrm{i}n\end{equation*}}{16\pi in}=(16\pi xin)/(16\pi in) \\ (6480\degree)/(16\pi)=x \\ 128.9\degree\approx x \\ \text{ The symbol }\approx\text{ is read 'approximately'.} \end{gathered}]()
Answer
The measure of the angle x rounded to the nearest tenth is 128.9°.