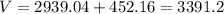1 Answer

EnriqueBet · Answer 1 · 2023-10-08T05:00:16+0000

Volume of the composite solid is the sum of the volume of the cylinder and volume of the hemisphere.

The radius of the cylinder is 12/2=6 cm

Height of the cylinder is 26 cm

Volume of the cylinder is given by

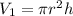
$V_1=\pi r^2h$

Hence the volume is given by

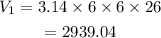
$\begin{gathered} V_1=3.14*6*6*26 \\ =2939.04 \end{gathered}$

Now the volume of the hemisphere is

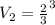
$V_2=(2)/(3)\pir^3$

Hence the volume of the hemisphere is

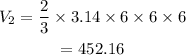
$\begin{gathered} V_2=(2)/(3)*3.14*6*6*6 \\ =452.16 \end{gathered}$

And the total volumeis

Please log in or register to add a comment.