Answer:
a)
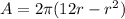
b)
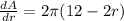
c) The value of r that maximizes A is r = 6cm
Step-by-step explanation:
We know that

We also want to find an expression for the curved area. This area is a rectangle with the length of the base equal to the circumference of the circle, and the height h.
The circumferece of a circle of radius r is:
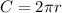
The the area of the rectangle is base times height:
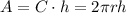
Now, since we want the area in terms of the radius, we can solve for h on relation we know between them:
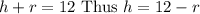
And now we can replace h in terms of x:
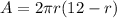
And we can apply the distributive property to make de differentiation easier:
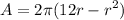
And that's the answer to item a.
For item b, we need to differentiate. We can do this first using this property:
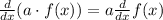
We can take out the 2π outside the differentiation.
Next, we can use the power rule:
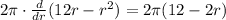
Thus, this is the answer to b
Finally, the item c ask us to find the radius when the area is maximized. When we have a derivative of a function, the x's where the derivative is zero, in the function there is a minimum or ma maximum.
In this case, we have a quadratic equation, and we know that this functions have only one maximum or only one minimum. SInce the principal coeficcient is negative (the one multiplying the r²) the parabolla ha it's "arms down" and in the vertex there is a maximum.
Then, let's find the sero of the derivative:

The radius for which the curved area is maximum is 6cm. Note that this means that
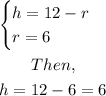
And the maximum is when r = h = 6. This makes the curved surface a square, and the square in the quadrilateral that maximizes the area for a given perimeter.