The question is given below as
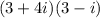
Concept:
Apply the complex arithmetic rule
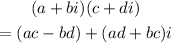
By comparing coefficient with the main question, we will have
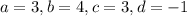
Step 1: Substitute the values in the arithmetic rule
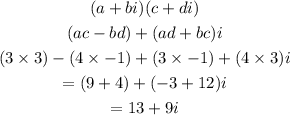
Alternatively,
Use the FOIL method
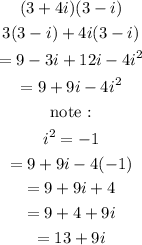
Hence,
The final answer is = 13 + 9i