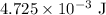Given data:
* The extension of the wire is 0.3 mm.
* The length of the wire is 4 m.
* The cross sectional area of the wire is,
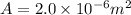
* The young modulus of the steel is,

Solution:
The young modulus of the steel wire in terms of the force acting on the wire is,
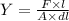
where A is the area of cross section, dl is the extension, l is the length of the wire, and F is the force acting on the wire,
Substituting the known values,
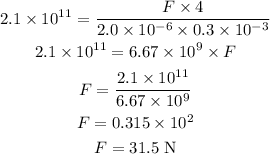
The energy stored in the stretched wire is,
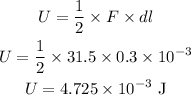
Thus, the energy stored in the stretched wire is,