Question

Consider the sequence (3, 8, 13, 18, 23, 28, 33...).7What is the value of E an?n=4O a.) 69O b.) 84O c.) 102d.) 126

Answer 1

The given sequence is

`\lbrace3,8,13,18,23,28,33,...\rbrace`

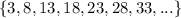
Since

8 - 3 = 5

13 - 8 = 5

23 - 18 = 5

Then it is an arithmetic sequence with common differences 5

We need to find

`\sum_{n\mathop{=}4}^7a_n`

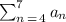
That means we need the sum of the terms from n = 4 to n = 7

The 4th term is 18

The 7th term is 33

Then the sum is

`\begin{gathered} S=18+23+28+33 \\ \\ S=102 \end{gathered}`

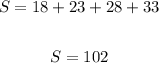
The answer is c