Question

A puzzle expert wrote a new sudoku puddle book.his initial costs are three hundred and twenty-five dollars.Binding and packaging each book costs sixty cents.The price of the book is one dollar and ninety cents.how many books must be sold to break even.enter an integer

Answer 1

The number of book that must be sold to break even are 250 books.

STEP - BY -STEP EXPLANATION

What to find?

The number of book that must be sold to break even.

Given:

• Initial cost of puddle book = $325

,

• Binding and packaging each book = 60 cents =$0.6

,

• The price of the book = $1.90

Let x be the number of books.

Cost of production C(x) = $325 + 0.6x

Revenue R(x) = Quantity of items * price

R(x) = x * 1.90 = 1.90x

To break even, the the Revenue must be equal to the cost of production, that is, there is neither profit nor loss.

This implies that:

R(x) = C(x)

1.90x = 325 + 0.6x

Subtract 0.6x from both-side of the equation.

`1.90x-0.6x=325+\cancel{0.6x}-\cancel{0.6x}`
`1.3x=325`

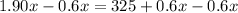
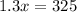
Divide both-side of the equation by 1.3

`\frac{\cancel{1.3}x}{\cancel{1.3}}=(325)/(1.3)`
`x=250`

Therefore, the number of books that must be sold to break even are 250