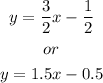Question

Hello could you please help me with these questions? Question 12.

Answer 1

The general form of the equation of a straight line in the slope-intercept form is given to be:

`y=mx+b`

where m is the slope of the line and b is the intercept on the y-axis, that is the y-value when x = 0.

To calculate the slope, we can use the formula:

`m=(y_2-y_1)/(x_2-x_1)`

From the question provided, we have the points:

`\begin{gathered} 1\Rightarrow(x_1,y_1)=(-1,-2) \\ 2\Rightarrow(x_2,y_2)=(3,4) \end{gathered}`

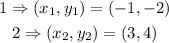
Using these values, we can calculate the slope to be:

`m=(4-(-2))/(3-(-1))=(4+2)/(3+1)=(6)/(4)=(3)/(2)`

Hence, we have the equation of the line to be:

`y=(3)/(2)x+b`

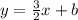
We currently do not have a value for b. We can find b, however, by substituting a point into the equation. Then we can solve for b. Using the second point, we have:

`\begin{gathered} 2\Rightarrow(x,y)=(3,4) \\ \therefore \\ 4=(3)/(2)(3)+b \\ 4=(9)/(2)+b \\ b=4-(9)/(2) \\ b=-(1)/(2) \end{gathered}`

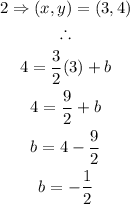
Therefore, the equation of the line is:

`\begin{gathered} y=(3)/(2)x-(1)/(2) \\ or \\ y=1.5x-0.5 \end{gathered}`