Question

Use this equation to write an equation that has many/infinite solutions, No solution and one solution:y=3x+4

Answer 1

Given the equation :

`y=3x+4`

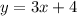
The slope of the line = 3

The intercept = 4

We need to write equation to satisfy each of the following :

1) the system has many/infinite solutions

So, we need to write equation with the same slope and the same intercepts

So, multiply the equation by any real number except ( 0 , 1 )

So, by multiplying the equation by 2

The equation will be:

2y = 6x + 8

2) The system has no solution

So, we need to write equation with the same slope and different intercept

So, the equation will be :

y = 3x + b

where b = any real number except 4

So, one of the equations will be : y = 3x + 2

3) the system has only one solution

So, we need to write equation with a different slope

So, the equation will be :

y = ax + 4

where : a is any real number except 3

So, one of the equations will be :

y = x + 4