Question

Sales people have average annual sales of 100000 with Standard Deviation of 10000. What percentage of the salespeople would be expected to make annual sales of 120000

Answer 1

Given:

mean/average = 100,000

Standard deviation = 10,000

raw data = 120,000

Find: the percentage of salespeople expected make an annual sale of 120,000

Solution:

To be able to get the percentage, we need to convert the raw value to z-score first. The formula is:

`z=\frac{x-\bar{x}}{\sigma}`

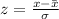
where x = raw data, bar x = mean, and σ = standard deviation.

Since we have those values in the given data, let's plug it in to the formula.

`z=(120,000-100,000)/(10,000)=(20,000)/(10,000)=2.00`

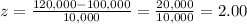
Hence, the z-score of the given raw data is 2.00.

Based on the standard normal distribution table, the area covered by z = 2.00 or greater is 0.0228.

Therefore, the percentage of the salespeople who are expected to make an annual sales of 120,000 is only 2.28%.