Question

Solve the following equation for all values of x, 0 ≤ x ≤ 2π2cos^2 (x) = cos(x)

Answer 1

we have the equation

`2cos^2x=cos\left(x\right)`

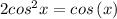
Simplify

`\begin{gathered} (2cos^2x)/(cos(x))=(cos\left(x\right))/(xos(x)) \\ 2cos(x)=1 \\ cos(x)=(1)/(2) \end{gathered}`

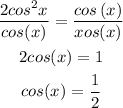
Remember that

`cos((pi)/(3))=(1)/(2)`

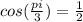
the value of the cosine is positive

that means

the angle x lies on the first quadrant and IV quadrant

For the First quadrant x=pi/3 radians

For the IV quadrant

x=2pi-pi/3

x=5pi/3 radians

therefore

In the given interval for x

the solutions are

x=pi/3 and 5pi/3