The equation of the line is given by:
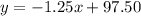
Since the slope is -1.25 it follows that the heating cost decreases by 1.25 for an increase of one degree Fahrenheit.
Therefore, for an increase of one degree Fahrenheit, the predicted decrease in monthly heating cost is $ 1.25
To find the predicted cost per month with an average temperature of 0°F, substitute x = 0 into the given equation:
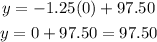
Therefore, the predicted cost per month with an average temperature of 0°F is $97.50
To find the predicted cost per month with an average temperature of 0°F, substitute x = 45 into the given equation:
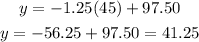
Therefore, the predicted cost per month with an average temperature of 0°F is $41.25