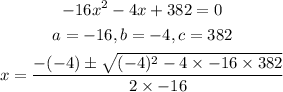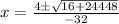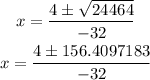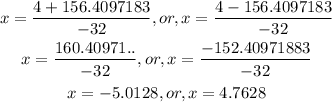Given: The function representing the distance, in feet, between the rock and the ground X seconds after it is thrown as
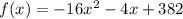
To Determine: How long after the rock is thrown does it hit the ground
Solution
Please note that when the rock hits the ground, the vertical distance f(x) would be zero
Therefore
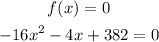
Solve for x in the equation using the quadratic formula
The quadratic formula is given as