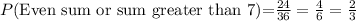First, we need to find the sample space for two dice. Since each dice has 6 faces, the sample space is
which consist in 36 elements.
Part A.
In this case, we need to find the combinations where the sum of the 2 dice is even. The combinations are:
for instance, in the upper left corner, the sum is 1+1=2, which is an even number and similarly for the other cases.
As we can note, there are 18 possible combinations. Then, the probability is
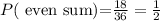
Part B.
In this case, we need to find the possible combinations where the sum of the 2 dices is greater than 7. The possible combinations are:
Since there are 15 possible combinations, the probability is given by

Part C.
This case is the intersection of the two cases from above. The possible combinations are:
Since there are 9 possible combinations, the probability is

Part D.
We need to find the possible combinations where the sum is even or the sum is greater than 7. Then, this case is the union of case A and B. Then the possible combinations are:
Since there are 18+6=24 combinations, the probability is