Question

If f(x)=5x^2-x-4 and g(x)=x-6What (f+g)(x)=And(f+g)(9)=

Answer 1

`\begin{gathered} (f+g)(x)=5x^(2)-10 \\ \left(f+g\right)\left(9\right)=395 \end{gathered}`

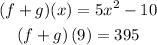
Step-by-step explanation

given

`\begin{gathered} f(x)=5x^2-x-4 \\ g(x)=x-6 \end{gathered}`

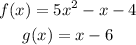
Step 1

a) (f+g) (x)

here we need to find a new function ( f+g) (x), this is the sum of the functions f and g, so to find it just add g(x) to f(x)

hence

`\begin{gathered} (f+g)(x)=5x^2-x-4+x-6 \\ add\text{ like terms} \\ (f+g)(x)=5x^2-10 \end{gathered}`

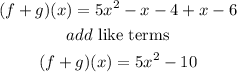
so

`(f+g)(x)=5x^(2)-10`

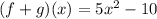
Step 2

now, we have to evaluate that function for x= 9

so

`\begin{gathered} (f+g)(x)=5x^(2)-10 \\ evaluate\text{ for x=9} \\ replace\text{ and calculate} \\ (f+g)(9)=5(9)^2-10 \\ (f+g)(9)=5(81)-10=405-10 \\ (f+g)(9)=395 \end{gathered}`

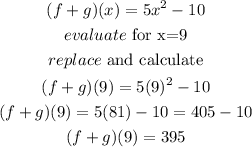
so

`(f+g)(9)=395`

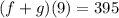
I hope this helps you