SOLUTION:
Step 1:
In this question, we are given the following:
Bismuth-210 has a half-life of about 6 days.
After 21 days, how many milligrams of a 1,220 mg sample will remain?
Round answer to the nearest tenth place.
Step 2:
The details of the solution are as follows:
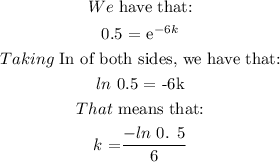
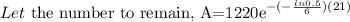
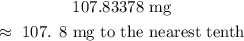
CONCLUSION:
The final answer is: