Answer:
5 rad /s
Step-by-step explanation:
The angular velocity is defined by
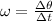
This means that the angular frequency is the slope of the θ vs. time graph.
Therefore, our original question is rephrased to the following.
What is the slope of the θ vs. time graph at t = 5s?
We find the slope using points (0, 25) and ( 5, 50).
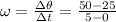
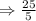
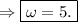
Hence, the angular frequency of the object is 5 radians/sec.