Question

Solve the rational equation for x and state all x values that are excluded from the solution set. If there is more than one excluded value then separate them with a comma and do not include any spaces. If a value is not an integer then type it as a decimal rounded to the nearest hundredth. \frac{5}{x+1}+\frac{1}{x-3}=\frac{-6}{x^2-2x-3} Solving for x gives us x=AnswerThe value for x cannot equal Answer

Answer 1

Solving for x gives us x = 1.33

The value for x cannot equal 3,-1

Step-by-step explanation:

The initial expression is:

`(5)/(x+1)+(1)/(x-3)=(-6)/(x^2-2x-3)`

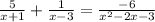
The denominator of the right side can be factorized as (x - 3)(x + 1) because -3 and 1 multiply to -3 and sum to -2. So, we can rewrite the expression as:

`(5)/(x+1)+(1)/(x-3)=(-6)/((x-3)(x+1))`

Now, we can sum the expression on the left side to get:

`\frac{5(x-3)+(x+1)}{(x-3)(x+1)_{}}=(-6)/((x-3)(x+1))`

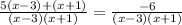
Both sides have a denominator of (x-3)(x+1), so we need to exclude the values where this denominator is equal to 0. Those values are:

x - 3 = 0

x - 3 + 3 = 0 + 3

x = 3

x + 1 = 0

x + 1 - 1 = 0 - 1

x = -1

So, the values of x cannot be equal to 3 and -1.

Then, if the denominators are the same, we can find the solution of the equation, making equal the numerators, so we need to solve:

`5(x-3)+(x+1)=-6`

Solving for x, we get:

`\begin{gathered} 5(x_{})+5(-3)+x+1=-6 \\ 5x-15+x+1=-6 \\ 6x-14=-6 \\ 6x-14+14=-6+14 \\ 6x=8 \\ (6x)/(6)=(8)/(6) \\ x=1.33 \end{gathered}`

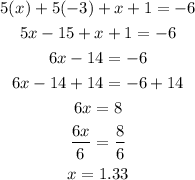
Therefore, the answers are:

Solving for x gives us x = 1.33

The value for x cannot equal 3,-1