We will investigate how to determine the probability of drawing an object from the given sample.
We have a pack of cards ( sample ), it contains 52 cards:

A pack of playing cards is distributed in terms of suits and colors as follows:

Every suit is further distributed in numerals and cardinals as follows:
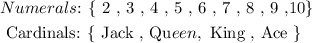
To determine the probability of any event we will consider the objects picked and the sample space from which they are picked. The ratio of the two is gives us the probability of the event to be a sucess!
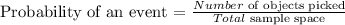
We will define our event as follows:

The number of objects picked:

We can now determine the probability of the event as follows:
