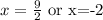Solution:
Given the equation:
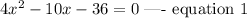
To solve using the quadratic formula, we have the solution of the quadratic equation:
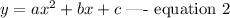
to be
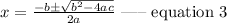
Comparing equations 1 and 2, we have
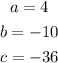
By substituting these values into equation 3, we have
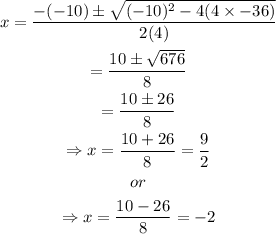
Hence, the solution, using the quadratic formula, is